来自日课:海森堡论不确定性
"像《蚁人》这类电影里主角变成蚂蚁大小,是否可以观察到原子呢?那么可以观察量子力学的世界吗?"
我们粗略地说,原子的势力范围直径大约在 10^(-10)米,人的直径大约是 1米。漫威设定蚁人的身高是 1 厘米,我们姑且就当他的直径是 1 毫米吧 —— 也就是 10^(-3)米。显然蚁人理我们更近,离量子力学很远。
蚁人感受到的物理效应会跟我们很不一样。比如他从高处掉下来不会摔坏,他很容易就能爬上墙,他会被风轻易吹飞……我们专栏以前讲过杰弗里·韦斯特的《规模》,不同尺度的生物生活方式很不一样。但是,蚁人跟量子力学没啥关系。
如果你想创作一个能涉及到量子力学现象的漫画电影,可以考虑写“病毒人”。病毒的直径是 10^(-8) 到 10^(-7)米,它能被分子尺度的热运动推着到处走,它能非常实在地感受到光子打在身上带来的疼痛,它眼中的原子很大 ……但是,严格来说它没有眼睛,因为它身上总共只有那么多原子,根本不足以形成特别复杂的结构。
"光子单缝实验中,它虽然会发散开来但为什么还会有深浅不一的条纹呢?单缝没有波的干涉啊?"
单缝和双缝没有本质区别,也会形成干涉。单缝的干涉来自从缝的不同位置出发的光波之间的干涉。下面这张图表现得非常明白 ——
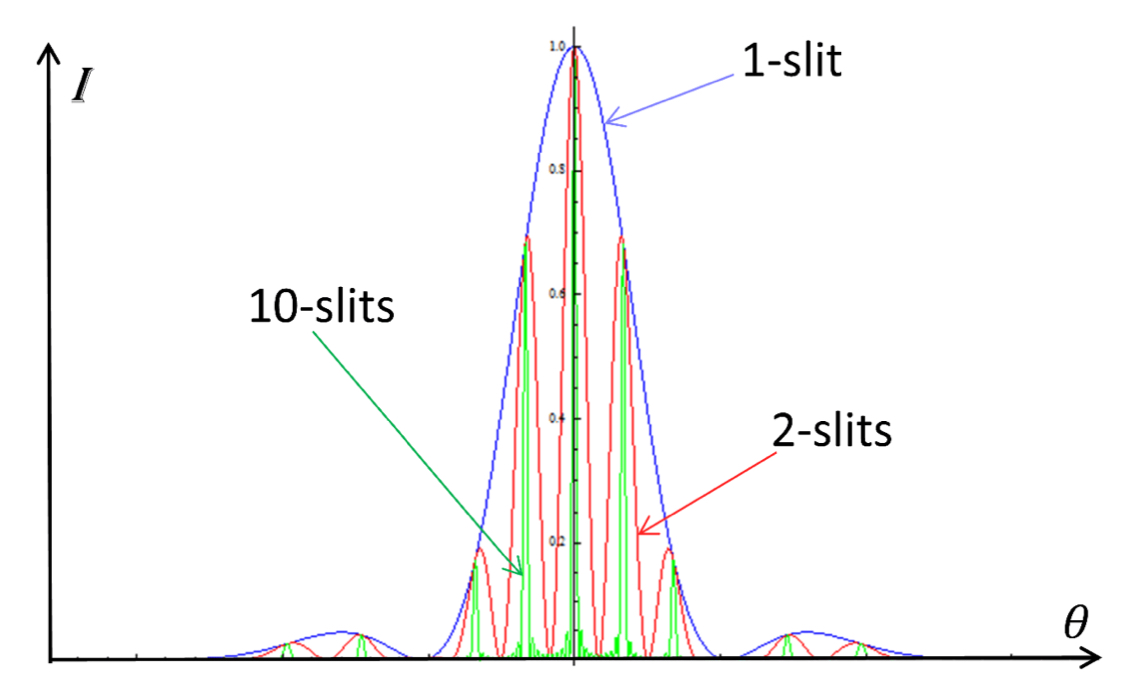
两条缝、或者 10 条缝的干涉条纹,都是单缝干涉条纹的“子集”。缝数增加,能获得更多的精细条纹结构,这是因为缝数多,光波的出发位置受到的限制就多,而干涉被别的位置掩盖的就少。
"我看到一个关于电子形状的测定,其中一个重要的步骤就是要把电子约束在一个确定的位置,并且通过这个实验还对电子的形状进行了极为精确的测定。这是否违背了不确定性原理?"
"如果电子和原子核都是“云”,怎么解释金箔撞击实验呢?"
"电子和原子核都是不确定的,但是组成的原子是确定的吗?"
"回旋加速器加速电子到很大的速度,从低速到高速的加速过程中到射出回旋加速器,也就是动量越来越大的过程中,科学家都可以很好的控制其位置,并且还么可以当子弹射向其他待研究的粒子,回旋加速器的过程中感觉电子这颗“子弹”的位置也可以精确知道啊,要不然速度大了动量大了,位置不确定了,也没法用它做研究啊,这是怎么回事?"
这些问题说的其实是同一件事:不确定性的“度”在哪里。不确定性原理是个*量化*的原理,我们再看一眼它的公式 ——
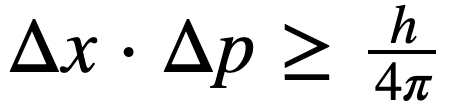
它并没有说电子的动量或者位置具有无限大的不确定性,它说的是动量不确定性乘以位置不确定性,这个乘积,不能比普朗克常数除以 4π 更小。而普朗克常数是一个非常非常微小的数字。
在回旋加速器和用阿尔法粒子轰击金箔的实验中,粒子的动量都已经很大了,动量一点点的误差都是很大的,那么对应之下,粒子位置的不确定性就可以是非常非常小的。高速的粒子就好像是宏观的粒子一样。
同样道理,原子的位置不确定性也很小。这是因为原子中有若干个质子和中子,而质子、中子的质量是电子的 1837 倍 —— 这就意味着在同样的速度上,质子、中子的位置不确定性要比电子小 1837 倍。跟电子相比,原子更像是宏观的粒子;正如跟光子相比,电子更像是宏观的粒子。
而即便对于电子,我们说它的不确定性也是在极其微观的量子尺度上说的。我们在宏观上完全可以说电子“精确地”出现在哪里:我手上的一个皮肤细胞中的水分子上有个电子,这个电子在哪里?它就精确地在我手上的一个皮肤细胞中的水分子上。
来自日课:薛定谔解出危险思想
"像薛定谔方程的解1+2i,它的绝对值平方如何表示概率呢?感觉这个数算出来就大于1了啊?"
真实计算的时候,解完方程还要来个“归一化”的处理,确保各地概率加起来的和等于 1。薛定谔方程本身并不在乎波函数的绝对值是大是小,把波函数扩大或者缩小多少倍,它还是方程的解。方程只在乎各个地区的波函数的相对大小关系。
而且因为波函数是个连续的函数,我们真实计算概率的时候不能说“电子出现在 x=1 这个点的概率”,我们只能说,比如“电子出现在 x=0.999 到 x=1.001 这一小段空间的概率”,而后者需要对波函数的绝对值的平方求积分。当我们谈论“位置”的时候,我们实际上总是谈论的是一段区间,而不是一个抽象的点。
"双缝实验里打在屏幕上的电子可以认为是电子的波函数坍缩后得到确定的“位置”,电子是被屏幕吸收了吗?如果有可能再捕捉到这个电子,它的不确定性还在吗?简单问就是:一个任意量子波函数坍缩后还有可能回到原来的概率叠加态吗?"
是的,电子跟屏幕上的感光物质发生了反应,形成了一个光斑,等于是被屏幕吸收了。在微观角度看来,电子接触到屏幕那一刻,它就等于是进入了下一个物理过程,前面那个自由飞行的过程就结束了,所以波函数必须发生改变。
我们如果把屏幕当做宏观的物体,就可以说电子原来的波函数已经坍缩了,或者说已经死了,不确定性消失了。它无法再回到原来的叠加态了。
而如果你不这么看,如果你把屏幕也当做一个量子力学尺度上的设备,感光过程也是量子过程,那就什么都是可逆的,波函数只是要改写而已,不确定性只是更新,而不是消失。
但光斑的出现是一个非常宏观的事件 —— 以至于都能让肉眼看到 —— 说明有大量的微观粒子参与了这个过程。那么这就是一个热力学事件,微观可逆,可是宏观上逆转的可能性非常非常小。就如同杯子摔在地上会碎,但是碎玻璃不太容易自发聚集起来变成一个好杯子。
来自日课:概率把不可能变成可能
"根据热力学第二定律,宇宙最后会达到热寂。能量不会再流动了。即使到那个状态了,还是不会有绝对静止的物体么?"
热寂的意思不是温度变成了 0,而是温度在各处都一样。宇宙中所有星体都散开,到处漂浮着一些基本粒子,这样的场景,并不代表它就是绝对零度。宇宙微波背景辐射仍然在,光子们仍然在,原子们仍然在震动,只不过没有什么有意义的能量流动了。
王小波描写热寂的话说,“将来的世界是银子的” —— 这是因为银子的导热性能特别好,意思就是温度到处都一样。这个意境并不美丽,但是原子们仍然在动。
"如果我们画第一个圈,代表数学世界;画第二个圈,代表真实世界。那么,这两个世界的圈应该是什么关系?完全重合吗,还是相互包含?如果是相互包含,那谁包含谁呢?"
"常听到,数学是一种精妙的、可以用来抽象化地描述物质的符号。仿佛有种先有物质后有数学的感觉。 而文中又谈到,狄拉克方程通过数学,“要求”反物质的存在。感觉似乎又变成了先有数学后有物质。 如何理解这种看似是“鸡生蛋还是蛋生鸡”的关系呢?"
真实世界这个圈很小,数学世界的圈很大,真实世界包含在数学世界之中。只要一种可能性在逻辑上没问题,它就是数学世界的一部分,它就有可能、甚至可以说一定会、在*某一个*宇宙中发生;但是在*我们的这个*宇宙之中,它未必发生。
数学不存在“诞生”的问题 —— 中国人没发现勾股定理的时候,勾股定理难道就不存在吗?勾股定理并不是因为我们而存在的,它一直存在。就算世界上没有人,甚至就算在宇宙起源之前,勾股定理就已经存在了。逻辑的存在不需要时间。
我们这个宇宙中的所有物质都起源于大爆炸,而大爆炸本身的发生、包括此后的每一步动作,都严密地符合数学。
来自日课:狄拉克统领量子电动力学
"如果电子经过了一个 z 方向上的磁场之后,引出了其中一束电子,再经过一个不与 z 方向垂直(非x方向)的磁场,会出现什么情况呢?"
一切都取决于夹角。假设那个新方向跟 z 的正方向的夹角是 θ,而你引出的电子是 z 的 + 自旋,那么它在新方向上仍然取值为 + 的系数是 cos(θ/2),概率则是这个系数的绝对值的平方,也就是 |cos(θ/2)|^2。
"对于文科生来说,抛开数学计算的公式,对于电子自旋和量子叠加态是否就很难做更深入的理解呢?"
我们总可以使用一些打比方的办法尽量体会量子力学在说什么,但是那些比喻必然会让理解变得模糊,而且会造成各种误解。
玻尔有句话说“如果一个人不为量子力学感到震惊,他就没有理解量子力学”;费曼有句话说“如果一个人说他理解量子力学,他就是没理解量子力学。”
如果你觉得量子力学就相当于日常生活中的什么东西如何如何,那就一定是错误的理解。这就如同翻译一样,中译英、英译中、梵文佛经翻译成中文或者英文,其中都有些词只有音译,因为实在找不到准确的对应。
而你只要稍微用一点数学,就能获得百倍的理解。


